為了降低渦輪流量計的始動流量qvmin,并降低儀表系數K較大的非線性,如何對非線性進行修正就是一個需要解決的重要問題。
根據國家計量檢定規程對速度式流量計檢定點的規定”,檢定點包括7個點,即qmin、0.07qmar、0.15qmar、0.25qmar.0.4qmar.0.7qmar和qmar檢定點的數量是有限的7個,而流量計在使用中,流量測量在qmin~qmax范圍內為任意的。這樣,流量計的檢定點和非檢定點就會遠遠超過7個。圖3給出了儀表.系數K與信號頻率F(或流量q)的典型非線性趨勢。
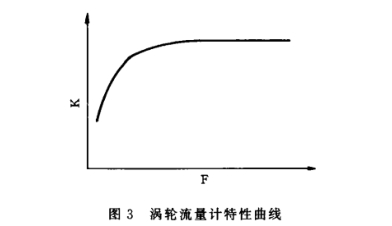
顯然不能再沿用平均儀表系數計算流量的方法,而應該用式(3)來計算在對應頻率信號F時的儀表系數K,再用式(2)計算流量。
K=f(F)(3)
該擬合公式的具體形式可用兩種方法求取,即折線法和最小二乘方法。
折線法是指將每兩個相鄰檢定點用直線相連接。顯然,在檢定點上,其擬合誤差為零,然而在非檢定點.上具有較大誤差。表1給出了一組典型的折線法非線性修正擬合數據。
擬合誤差的計算公式8]為:

從表1可見,在非檢定點處的最大擬合誤差達到±1.65%。
最小二乘方法得到的是一條連續曲線,其原則是使各檢定點到該曲線的誤差平方和為最小。由于檢定點上得到的數據并非標準值,其本身也具有一定的誤差,而且實際使用的渦輪流量計K-F特性曲線應該是連續的、平滑的,因此盡管在檢定點處的擬合誤差不一定等于零,但用最小二乘方法得到的連續曲線應該能更好地反映K-F關系的本質9]。表2給出了用最小二乘方法得出的一組非線性修正擬合誤差數據。
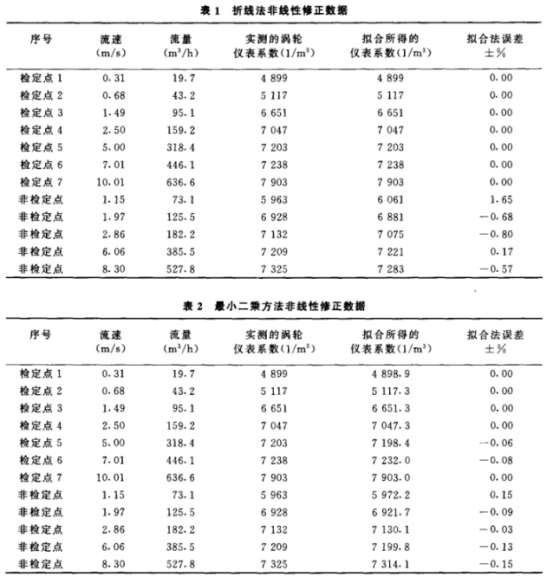
由表2可見,最大擬合誤差僅為±0.15%,遠優于折線法的擬合誤差結果。 |


