1.聲路角誤差修正
由于直接測量超聲波流量計角度較為困難,且其測量儀器精度不能達到要求,因此考慮在測量方式上進行優化,提出一種依據長度安裝要求達到控制聲路角的方法。

圖4所示為流量相對誤差與聲路角的關系。由圖4可知,在聲路角測量誤差較小時,流量測量相對誤差隨聲路角(安裝角)大小的變化不明顯,如圖中紅線(σθ=0.1%)所示。反之,若聲路角測量誤差較大,則流量相對誤差隨聲路角的變化呈拋物線變化,如圖中綠線(σθ=1°)所示,且存在一個最小值。聲路角不變時,流量相對誤差會隨著絕對誤差的增大而增大。
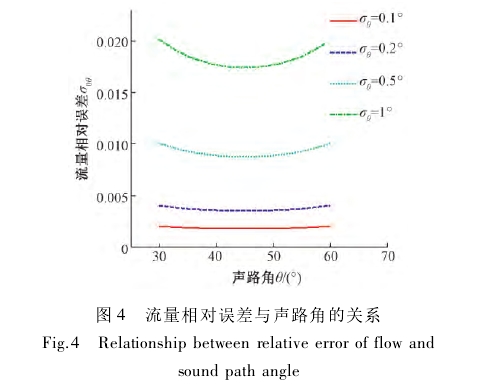
令შσ/შθ=0,有θ=45°時,流量的相對誤差σ0Q取最小。
2.K值的修正
K系數與流體型態有關且隨雷諾數變化而變化,研究不同型態下的K系數隨雷諾數變化規律有利于流量補償計算和提高測量精度。
由式(24)可知,層流時的修正系數K=4/3,但對大管徑來說,場內流態一般是紊流情況。因此,本文重點分析紊流時的超聲波流量計系數K的修正。
紊流時修正系數與雷諾數有關,經驗公式為:
K=1.119-0.011xlgRe(25)
依據式(25)可知.流量系數與雷諾數呈線性關系,雷諾數變化直接影響流量系數的取值。本文考慮根據雷諾數相關的變量來對K值進行修正。雷諾數計算公式為:

式中:V為平均流速;D為管道內經;Ƴ為流體運動粘度。
由式(26)可知,雷諾數大小與3個變量有關。當管徑一定時,雷諾數會隨著平均流速和流體粘度變化而變化。水的粘度隨溫度的變化而變化,溫度變化會影響到雷諾數,進而影響流量修正系數K的值。因此找出粘度隨溫度的變化關系對K的準確性有著一定的影響。
流體粘度受流體溫度的影響具有非線性特點,通過擬合溫度與運動粘度值,得到不同溫度下水的運動粘度的曲線,如圖5所示。
多項式擬合表達式為:
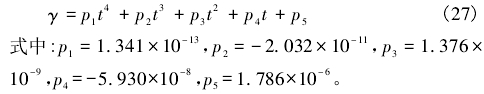
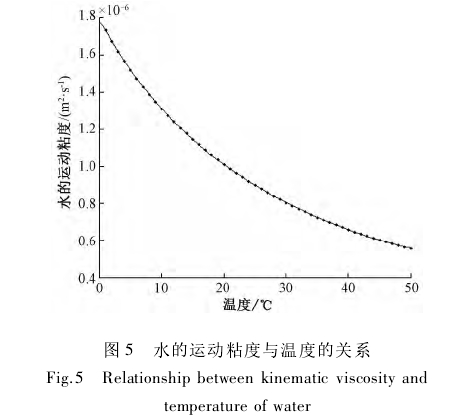
隨著溫度的升高,水的粘度非線性特征愈發明顯。在0~50℃范圍內水的粘度值差值可達到1.2x10-6m2/s,對應的雷諾數誤差為66.67%,不容忽視。
將得到的擬合曲線依次代入式(19)、(20)得:
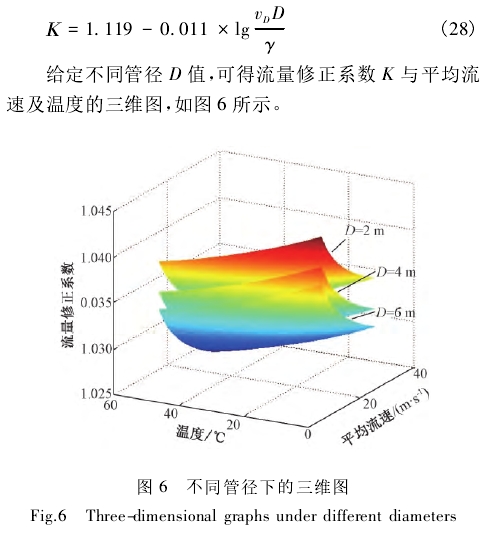
由圖6可以看出,同一管徑條件下,超聲波流量計系數隨平均流速和溫度的增加都呈非線性減小趨勢。其他條件一定時,隨著管徑D的增大流量系數K值會減小。
此修正方法將溫度和流速變化與K值聯系起來,兩者任一值發生變化都能找到相對應的修正系數值,為準.確測得流量提供了一定的理論基礎。 |


